ltleft.blogg.se - 2d projectile motion equations

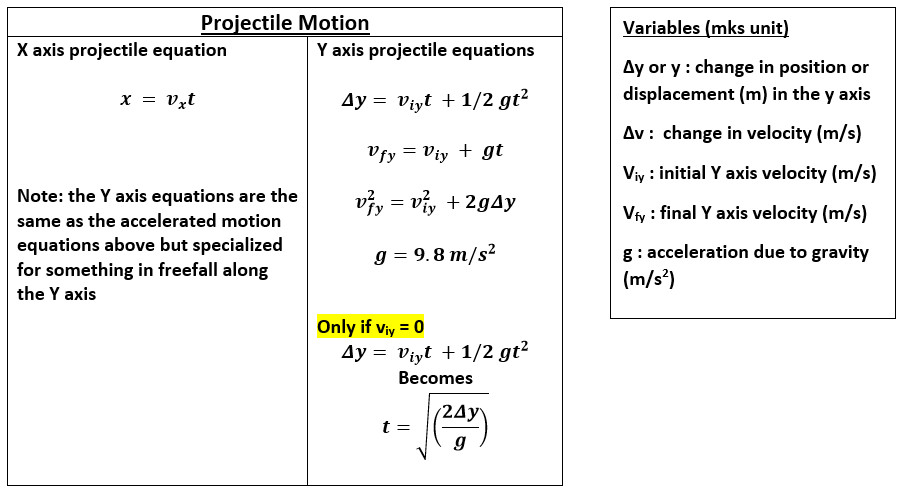
The above equations work well for motion in one-dimension, but a projectile is usually moving in two dimensions - both horizontally and vertically. Three common kinematic equations that will be used for both type of problems include the following:Įquations for the Horizontal Motion of a Projectile In this part of Lesson 2, we will focus on the first type of problem - sometimes referred to as horizontally launched projectile problems. The second problem type will be the subject of the next part of Lesson 2. Determine the time of flight, the horizontal distance, and the peak height of the long-jumper. A long jumper leaves the ground with an initial velocity of 12 m/s at an angle of 28-degrees above the horizontal.Determine the time of flight, the horizontal distance, and the peak height of the football. A football is kicked with an initial velocity of 25 m/s at an angle of 45-degrees with the horizontal.Predictable unknowns include the time of flight, the horizontal range, and the height of the projectile when it is at its peak. Upon reaching the peak, the projectile falls with a motion that is symmetrical to its path upwards to the peak. Determine the initial horizontal velocity of the soccer ball.Ī projectile is launched at an angle to the horizontal and rises upwards to a peak while moving horizontally. A soccer ball is kicked horizontally off a 22.0-meter high hill and lands a distance of 35.0 meters from the edge of the hill.

Predict the time required for the pool ball to fall to the ground and the horizontal distance between the table's edge and the ball's landing location.

A pool ball leaves a 0.60-meter high table with an initial horizontal velocity of 2.4 m/s.

Predictable unknowns include the initial speed of the projectile, the initial height of the projectile, the time of flight, and the horizontal distance of the projectile. The two types of problems are: Problem Type 1:Ī projectile is launched with an initial horizontal velocity from an elevated position and follows a parabolic path to the ground. While the general principles are the same for each type of problem, the approach will vary due to the fact the problems differ in terms of their initial conditions. There are two basic types of projectile problems that we will discuss in this course. In a typical physics class, the predictive ability of the principles and formulas are most often demonstrated in word story problems known as projectile problems. Combining the two allows one to make predictions concerning the motion of a projectile. The mathematical formulas that are used are commonly referred to as kinematic equations. The physical principles that must be applied are those discussed previously in Lesson 2. In the case of projectiles, a student of physics can use information about the initial velocity and position of a projectile to predict such things as how much time the projectile is in the air and how far the projectile will go. Such predictions are made through the application of physical principles and mathematical formulas to a given set of initial conditions.

Motion in any given direction is independent of motion in a perpendicular direction.One of the powers of physics is its ability to use physics principles to make predictions about the final outcome of a moving object.

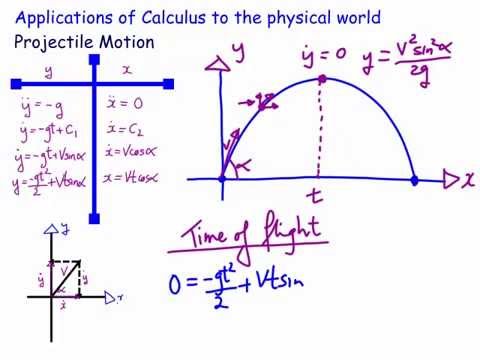
\)(t) can be written as a vector sum of the one-dimensional velocities v x(t), v y(t), v z(t) along the x, y, and z directions.